DFS+BFS Numberingで部分木の任意深さのクエリを処理する

Last updated Mar 24, 2020

Algorithm

Tree Depth Query by BFS Numberingについては Tree Depth Query by BFS Numbering - niuez.github.ioを参照してください.

# 処理したいクエリ (例)

有向木が与えられ, 各頂点には重みがある.

頂点$v$から, 辺をちょうど$d$個たどって到達できる頂点の重みの総和を出力

総和じゃなくても更新とかもしたいよね.

# アルゴリズム

BFS Numberingをすると, 同じ深さの頂点が並ぶということは上の記事をみるとわかります. これにDFS Euler Tourしたときの情報を合わせることで任意深さについで, BFS Euler Tourしたときの区間を前計算$O(N)$, クエリ$O(\log N)$で求めることができます.

がぞう

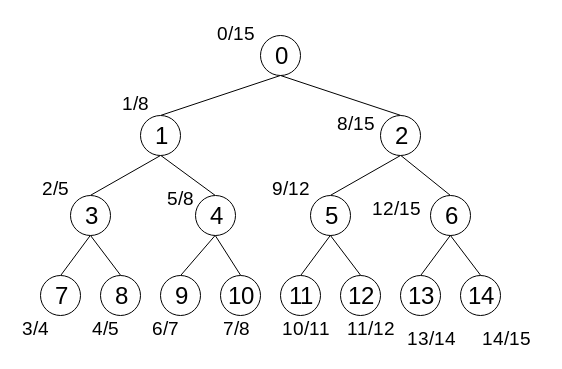
BFS Numberingしたときの順番と, DFS Numberingしたときの$in/out$を各ノードに添えました. ただし, ノードの子供を探索する順序はDFS, BFS共に同じにします, すると,

深さ$0$のノードのbfsの番号と$in$

1
2
bfs: 0
in : 0

深さ$1$のノードのbfsの番号と$in$

1
2
bfs: 1 2
in : 1 8

深さ$2$のノードのbfsの番号と$in$

1
2
bfs: 3 4 5 6
in : 2 5 9 12

深さ$3$のノードのbfsの番号と$in$

1
2
bfs: 7 8 9 10 11 12 13 14
in : 3 4 6 7  10 11 13 14

となり, 単調増加します.
また, DFS Numberingでは, ある頂点$v$の$[in, out)$は, $v$を根とする部分木に含まれる頂点の$in$の集合です. これを活かして, 頂点$1$から深さ$2$の頂点のBFS Numberingの区間を求めてみます.

木全体での頂点$1$の深さは$1$なので, 求めたい区間の頂点は深さ$3$です.
また, 頂点$1$の$[in, out)$は$[1, 8)$です. なので求めたい頂点の$in$の値は, 深さ$3$での$in$の列の中で$[1, 8)$に含まれている$in = 3, 4, 6, 7$です.
これは, BFS Numberingの区間では$[7, 10)$に相当します.

この操作は二分探索で行うことができるので, クエリあたり$O(\log N)$です.

# 実装

para[i] := BFS Numberingでi番目の頂点
inv_para[v] := BFS Numberingにおける頂点vのインデックス

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
struct bfs_euler_tour {
  int N;
  std::vector<std::vector<int>> G;
  std::vector<int> in;
  std::vector<int> out;
  std::vector<int> para;
  std::vector<int> inv_para;
  std::vector<int> dep;
  std::vector<int> par;
  std::vector<int> start;
  int cnt;
  int D;

  bfs_euler_tour(int N): N(N), G(N), in(N), out(N), para(N, -1), inv_para(N, -1), dep(N), par(N) {}

  void add_edge(int a, int b) {
    G[a].push_back(b);
    G[b].push_back(a);
  }

  void dfs(int v, int f, int depth) {
    D = std::max(D, depth);
    par[v] = f;
    dep[v] = depth;
    in[v] = cnt++;
    for(auto t: G[v]) {
      if(t == f) continue;
      dfs(t, v, depth + 1);
    }
    out[v] = cnt;
  }

  void build(int r) {
    cnt = 0;
    D = 0;
    dfs(r, -1, 0);
    D++;

    cnt = 0;
    std::vector<int> que(N);
    int ql = 0;
    int qr = 0;
    que[qr++] = r;
    start.resize(D + 1);

    for(int d = 0; ql < qr; d++) {
      int r = qr;
      start[d] = cnt;
      while(ql < r) {
        int v = que[ql++];
        inv_para[v] = cnt;
        para[cnt++] = v;
        for(auto t: G[v]) {
          if(in[v] < in[t]) {
            que[qr++] = t;
          }
        }
      }
    }
    start[D] = cnt;
  }

  int para_lower_bound(int l, int r, int i) {
    while(r - l > 1) {
      int m = (l + r) >> 1;
      if(i <= in[para[m]]) {
        r = m;
      }
      else {
        l = m;
      }
    }
    return r;
  }

  std::pair<int, int> range(int v, int d) {
    if(dep[v] + d < D) {
      int l = start[dep[v] + d];
      int r = start[dep[v] + d + 1];
      return { para_lower_bound(l - 1, r, in[v]), para_lower_bound(l - 1, r, out[v]) };
    }
    else {
      return { 0, 0 };
    }
  }
};

# 使用例

No.899 γathereeを解いてみました. #448690 (C++14) No.899 γatheree - yukicoder

# verify問題

びーと, ありがとう