Toptree 導入編
みんな日本語記事を待っていたはず….!
toptreeがどんな感じで動いているのかを書いてみます
実装はここにあります
https://github.com/niuez/toptree-rust
# 0. toptree is なに
toptreeはlink-cut treeの上位互換です. 木を切ったりつなげたり, パスのクエリを処理したり, 木上の二分探索ができたりします
今回はそのベースとなる構造の話です
# 1. Compress Rake
# 木をまとめる
ここで言う木は, toptreeが表す木のことです. 曖昧にならないようにこのことをreal treeと呼ぶことにします. (木を木で表現するの文章が曖昧になりがち)
toptreeでは, つながっている2つの辺をまとめる操作を繰り返したものを表現した木です. 1つの辺にまとめ上げることでパスを表現します.
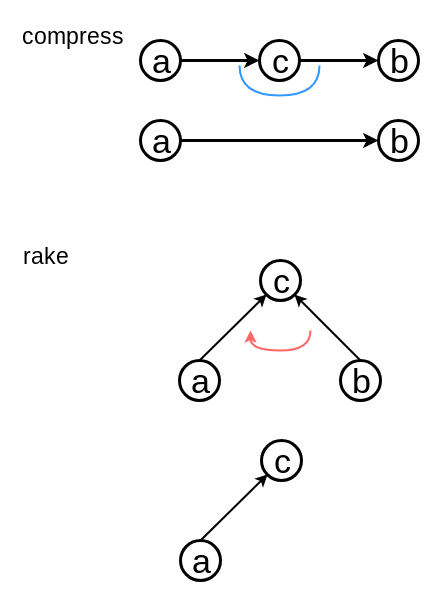
まとめる操作は2つあり, それぞれCompress, Rakeといいます.
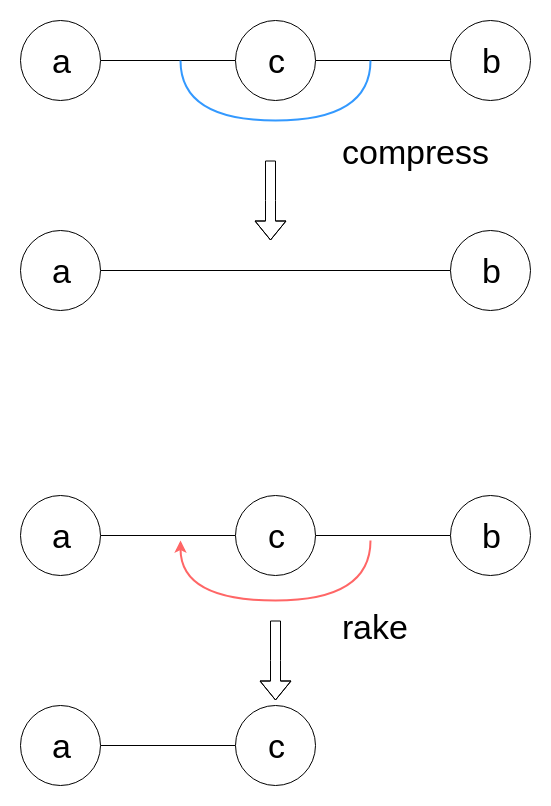
# 具体的に
こんな感じでまとめていきます
このまとめていく操作を木で表現するのがtoptreeです.
# Compress Tree
例えば, a - c - bという一直線のreal treeを扱う時, 辺acとcbをcompressをします.
これをtoptreeで表現すると
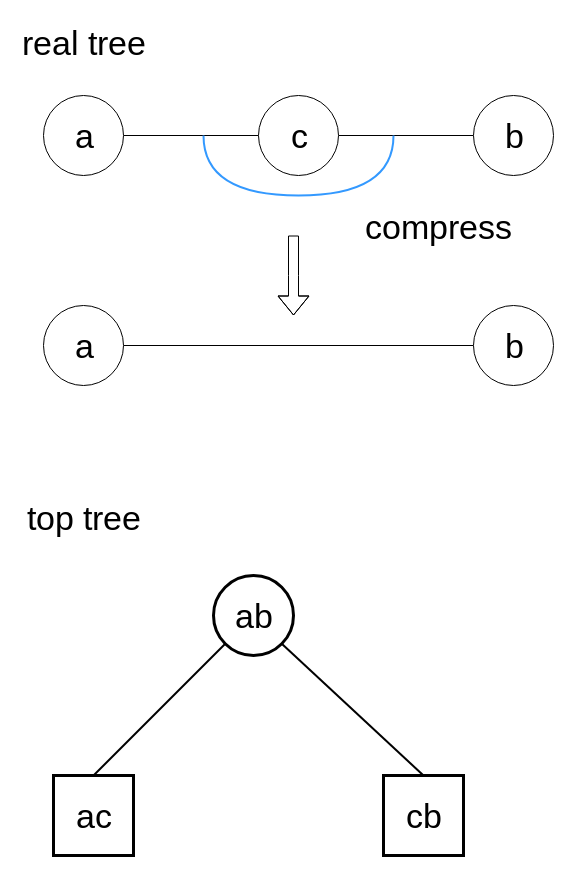
四角は辺を表すノードです. Edge Nodeといいます. toptreeでは, Edge Nodeを葉にします.
丸はcompressした後の辺を表すノードです. Compress Nodeといいます.
Compress Nodeが節, Edge Nodeが葉のこの木をCompress Treeといいます.
重要なのは, Compress Treeの根がパスの端点を結ぶ, Compressされた辺を表しているということです. またそのcompressされた辺の端点は必ず次数が1です.
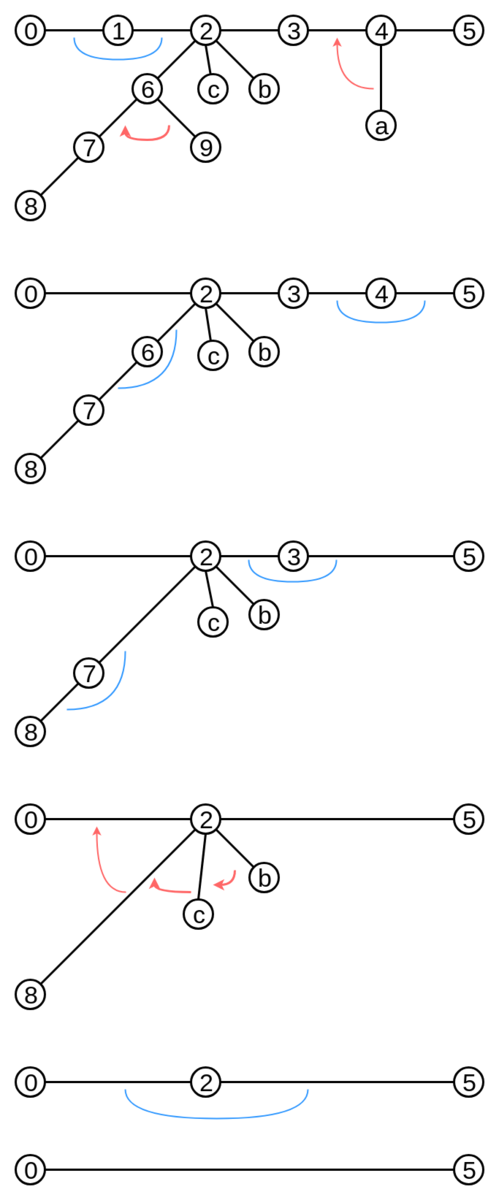
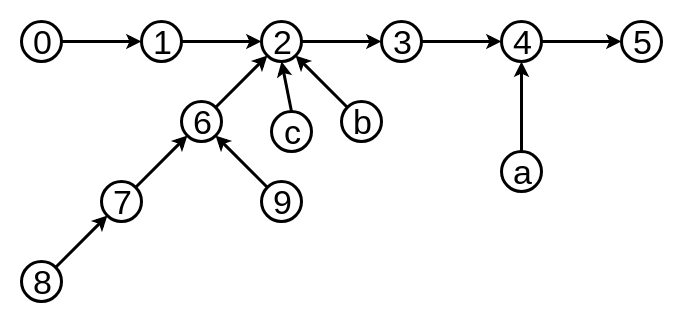
0 - 1 - 2 - 3 - 4 - 5 というreal treeをtoptreeで表すと, 一例としては以下のようになります.
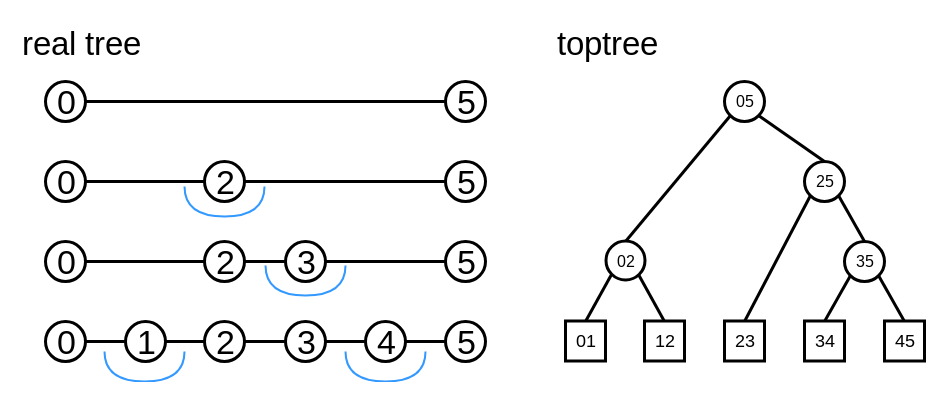
# 辺の向き付け
ここで葉のEdge Nodeの順番がパスの辺の順番になっている点に注意してください.
toptreeでは辺の向きに注意して操作しないとダメです.
僕の実装では, 0 - 1 - 2 - 3 - 4 - 5のtoptreeを0 -> 1 -> 2 -> 3 -> 4 -> 5と向き付けると解釈しています. 以後のreal treeの図では向き付けしたものを用います.
compress, rakeを, 同じ向きのものをまとめる操作と解釈することにしましょう. すると, compress, rakeを向き付けたreal treeについて改めて考えると以下のようになります.
上の具体的にで示したreal treeはこんな感じで向き付けすると同じようにまとめる操作ができるはずです.
# Rake Tree
では一直線ではないreal tree, 例えばこれはどうやってtoptreeにするのでしょうか.
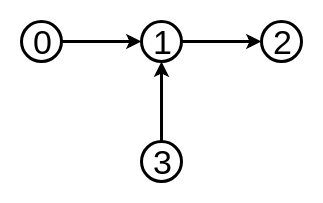
ここでrakeを使います.
?????????????????????
辺14を追加したreal treeをtoptreeにすると
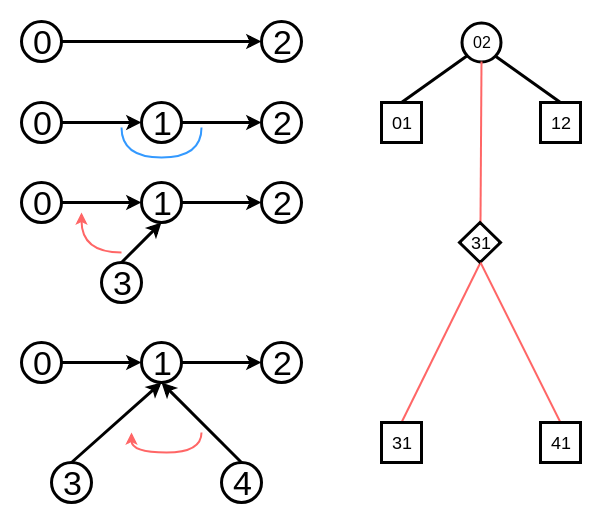
ひし形のノードはcompressと同じように察せるはずです. 31と41をrakeしたものを表現しており, ひし形のノードをRake Nodeといいます.
また, Rake Nodeが節, Compress Treeの根が葉の木をRake Treeといいます.
図では, Compress Nodeに今までの左右の子と, 赤の線でつながった子があります.
赤の線でつながった子は, Compress Nodeの右の子とrakeされるノードです.
このように3分木にしてreal treeの情報を持ちます.
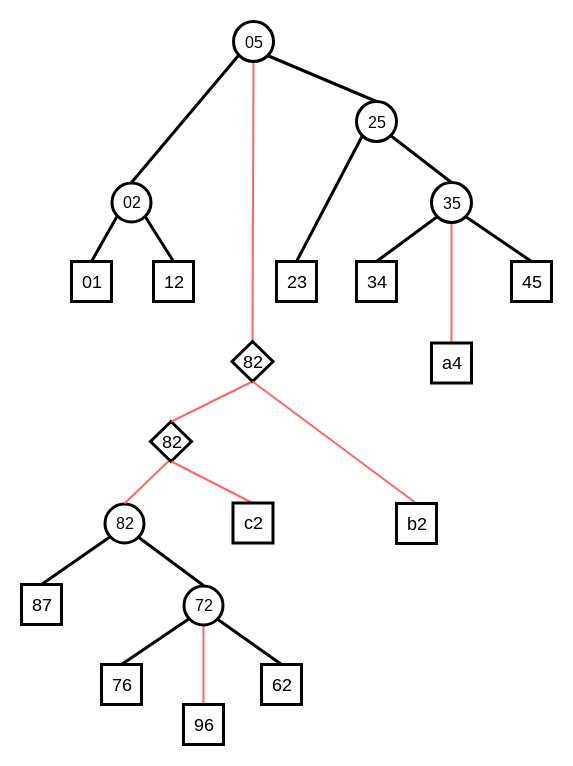
# 具体例のtoptree
こんな感じになります
四角はEdge Node, 丸はCompress Node, ひし形はRakeNodeです.
Compress Tree(青の点線で囲った部分), Rake Tree(赤の点線で囲った部分)はそれぞれここです
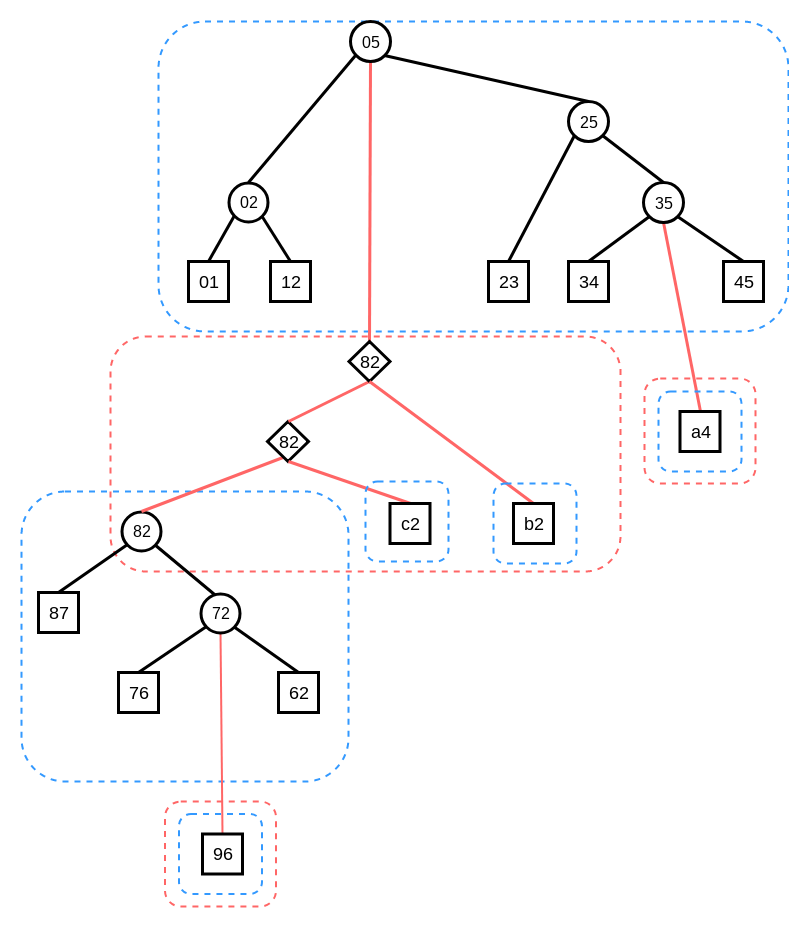
# Splice
重要なのは, Compress Treeの根がパスの端点を結ぶ, Compressされた辺を表しているということです.

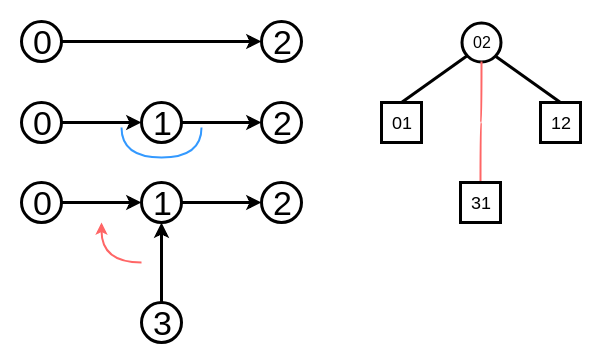
この木のtoptreeをもう一度見てみます.

0 - 1 - 2がこのtoptreeの主役のパスになっています.
でも, 3 - 1 - 2を主役にしたいときもあるはずです. それは, 31と01を入れ替えることで達成できます.
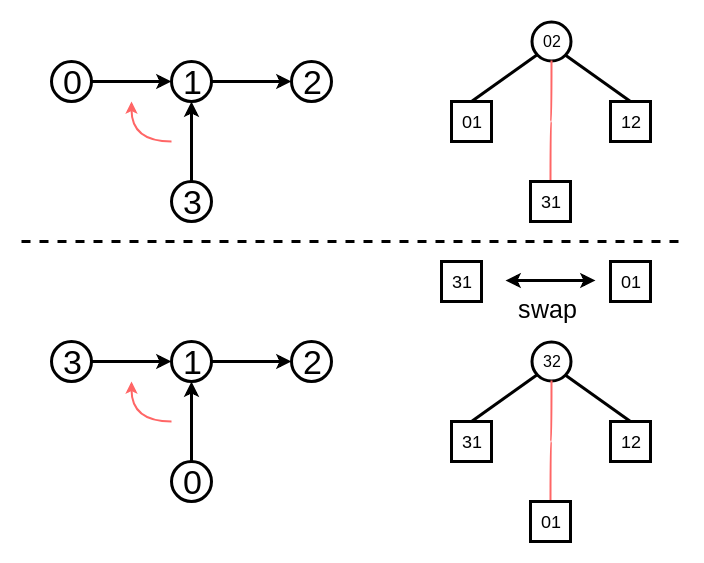
0 - 1 - 3にを主役にしたいときもあるはずです. それは, 31と12の向きを反転させてから入れ替えることで達成できます.
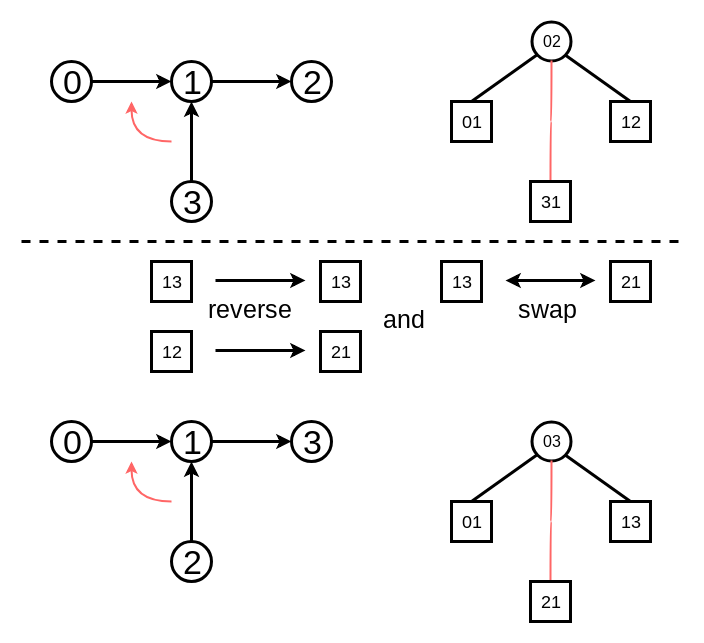
この, Rake Treeの葉のノードと, Compress nodeの子を入れ替えてCompress Nodeの表すパスを変える操作をspliceといいます.
# Splay
Splay Treeを知っていますか? wikipediaを見て
Splay Treeでは, splayという木を回転させてノードを根に持ってくるという操作をします. まあwikipediaみて
toptreeで扱っている木は, 葉木です. 葉はsplayできないことに注意しましょう.
# Handle
spliceをするとパスを変形できることはわかりましたが, 具体的にどのノードをspliceすると良いのでしょうか?
それを示すのがhandleという概念です. handleは各頂点に対して割り振られるもので, toptree上のCompress/Edge Nodeが割り振られます.
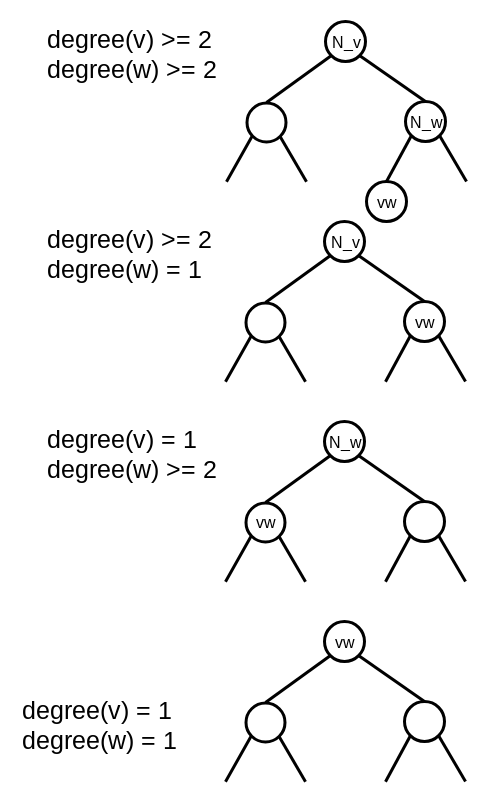
具体的には, 下のルールで構成します.
- Compress Node
abの左右の子がac,cbのとき, 頂点cのhandleはCompress Nodeab - Compress/Edge Node
abの親がいない(toptreeの根): 頂点a,bのhandleはCompress Nodeab - それ以外(Rake Treeの葉になっている): 頂点
aのhandleはCompress Nodeab
具体例を見たほうが早い気がします.
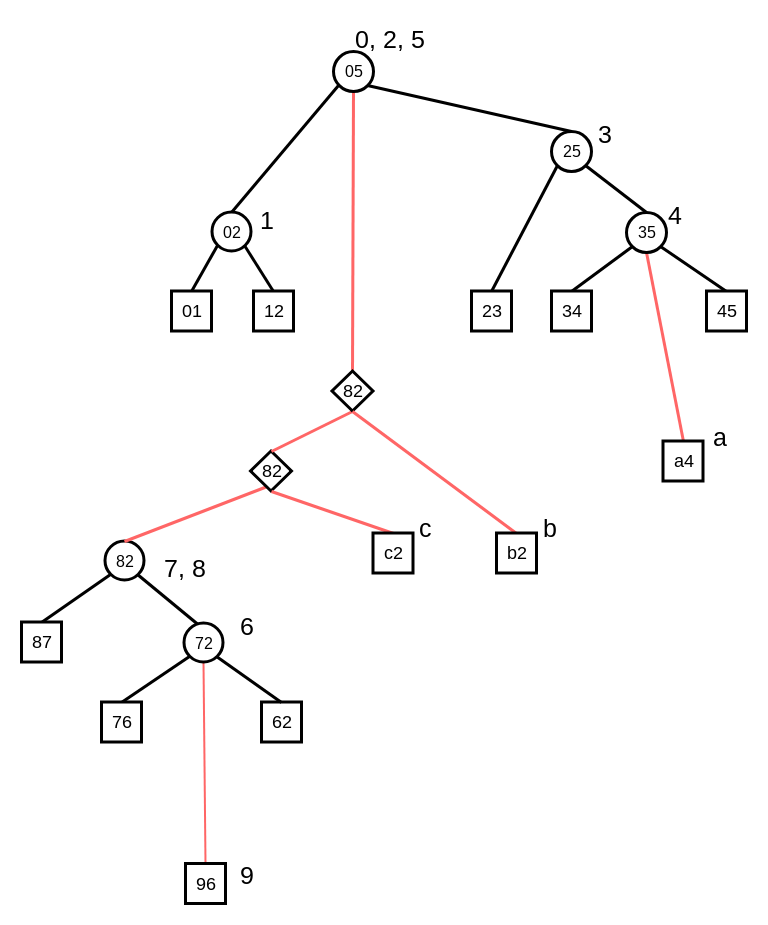
頂点0, 5はルール2., 8, a, b, cはルール3., それ以外は1.です.
今はとりあえずこういうものとしておくのがいいと思います.(あとで大活躍します.)
また頂点vに対して, N_vをvのhandleのNodeとします. (上の図で言えばN_2はtoptreeの根です)
# Expose
exposeという操作を導入したいと思います. (これが超本質)
任意の頂点vのhandleをtoptreeの根にするのがexposeです.
先にどうやってexposeするか書いてしまいます.
expose(v)
N_vをCompress Tree上でsplayするN_vの親が
- いない:
N_vはtoptreeの根になったのでexpose終了 - Compress Node: そのCompress Nodeを
nとおく - Rake Node: そのRake Nodeを
rとおく,rをRake Tree上でsplayし,rの親をnとおく(nはCompress Nodeになります)
nをCompress Tree上でsplaynの左のノードとN_vを入れ替えるN_vがEdge Nodeのとき,N_vをnにする- 1に戻る.
# 1. splay(N_v)
N_vの属しているCompress Tree上でN_vを根にします.
# 2.
これがちょっとむずかしいです.
親がいない場合は目的達成なので終了です.
Compress Nodeの場合, こんな状態です.
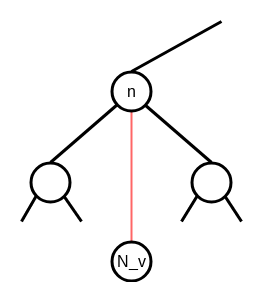
Rake Nodeの場合, 例えばこんな状態です.
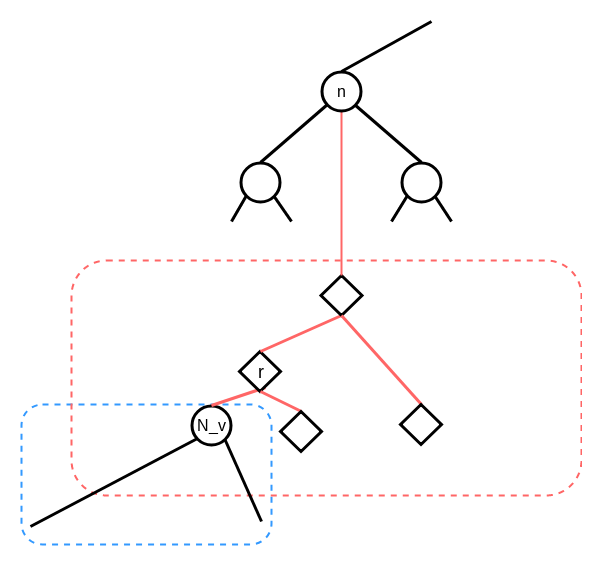
splay(r)をすると, こうなります.
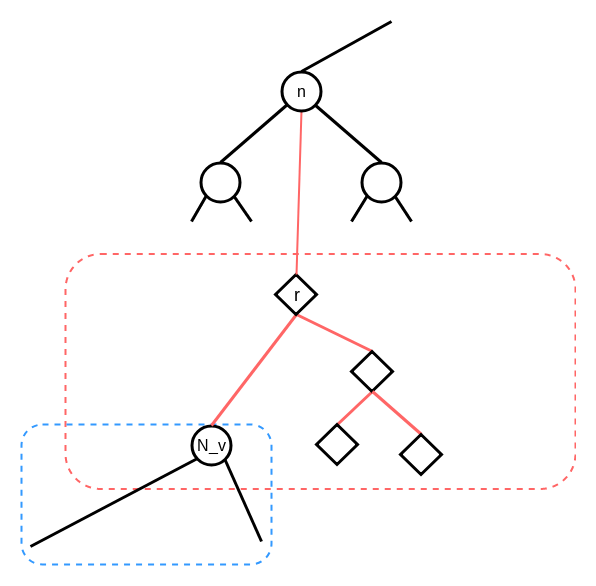
# 3. splay(n)
4で行う操作を簡単にするために行います. なんで簡単になるかはsoft_exposeで解説したいと思います.
# 4. splice(N_v)
入れ替えます.
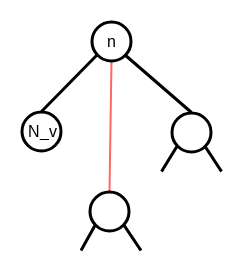
# 5.
これは何かというと, N_vがEdge Nodeのとき, spliceするとvのhandleの位置が変わります. これに対応するためです.
# 6.
これで, N_vをtoptreeの根にすることができます.
# Soft Expose
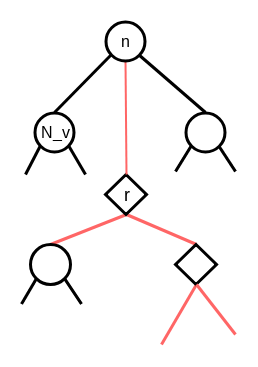
soft_exposeは任意の頂点v, w間のパスのCompress Node vwを作る操作です!(やっとここまできた)
こんな形にtoptreeを変形します.
(8/5 なんか頭悪い画像になっていたので修正しました)
手順を先に言ってしまいます
soft_expose(v, w)
expose(v)N_vとN_wが
- 同じ: toptreeの根は
vwかwvなので,wvであれば反転する.soft_exposeおわり - 違う: 続く
N_vをguardする(????)- expose(w)
N_vのguardを外すN_vから見てN_wが右側なら, 反転させる.- おわり
toptreeの根をguardするとは, splay操作があってもtoptreeの根を変えさせないようにすることです.
これは, N_vをtoptreeの根にした後, N_vの左側にN_wを持ってくる必要があり, N_vが根であり続ける必要があるからです.
guardされているときのspliceの操作が少し違います.
nの親がguardされていて, 親から見て左側にある場合, spliceはnの左の子と交換しないといけません.
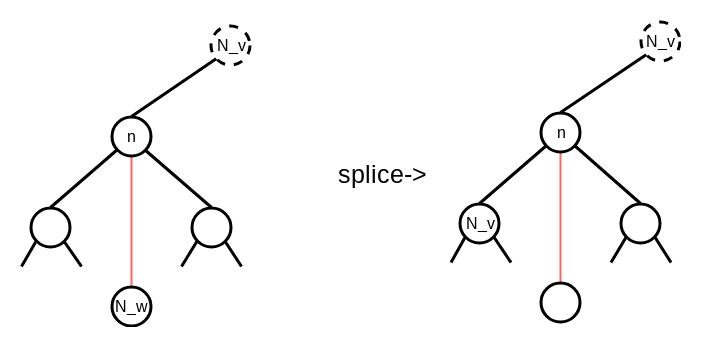
しかし, 親から見て右側にある場合, spliceはnの左の子と交換しないといけません.
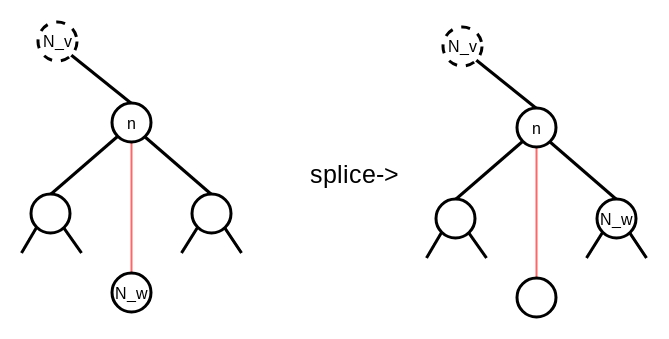
これはtoptreeの, 葉がパスの辺の順番になっているルールに違反するからです.(toptree壊れる)
# Path Query
soft_exposeができるようになると, パスに関するクエリを処理することができます.
パスの長さとか, パス中の辺の長さの最大値とかです.
各ノードに情報をもたせて, セグ木みたいに左の子の情報と右の子の情報を演算するみたいな感じです. これをすると, soft_expose(v, w)をしてvwを見た時にパスv-wについての演算結果が求まるはずです. やったね.
# ひとまず終了…
link, cut, select, 各種クエリとかは後日にします… 疲れた…
Toptree - Link & Cut編 - niuez’s diary link cutかいた
僕が書くのサボった厳密な話をnoshi91さんが書いています こちらも読んでください