BFS Numbering

Last updated Oct 5, 2019

Algorithm

僕が木上クエリコンで出題した問題で使った手法です.

# アルゴリズム

例

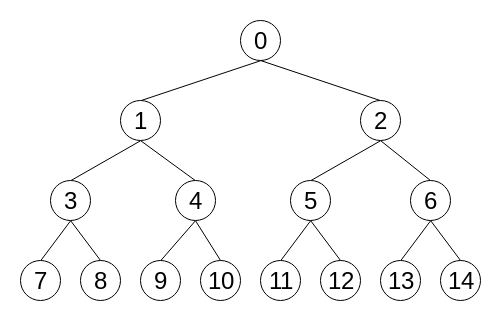
BFSを行って頂点に番号を順番に振っていきます.

1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

になります. ここで, BFSは深さが浅い順に頂点を見ることに注目すると,

頂点0の部分木の中で, 頂点0から距離1にある頂点

1
0 [1 2] 3 4 5 6 7 8 9 10 11 12 13 14

頂点0の部分木の中で, 頂点0から距離2にある頂点

1
0 1 2 [3 4 5 6] 7 8 9 10 11 12 13 14

また同様に

頂点1の部分木の中で, 頂点0から距離1にある頂点

1
0 1 2 [3 4] 5 6 7 8 9 10 11 12 13 14

頂点1の部分木の中で, 頂点0から距離2にある頂点

1
0 1 2 3 4 5 6 [7 8 9 10] 11 12 13 14

つまりBFS Numberingは, 深さを同じくする頂点を列の区間に落とし込むことができます.

実装はこんな感じ(この例では, 距離2までの頂点を記録しています)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
i64 N;
cin >> N;
idx.resize(N + 1, -1);//idx[v] := Euler Tourの列での頂点vの位置
L1.resize(N + 1, -1);//距離1にある頂点の列の左端
R1.resize(N + 1, -1);//右端
L2.resize(N + 1, -1);//距離2にある頂点の列の左端
R2.resize(N + 1, -1);//右端
p.resize(N + 1, -1);//親
G.resize(N + 1);
for(int i = 0;i &lt; N - 1; i++) {
  i64 a, b;
  cin >> a >> b;
  G[a].push_back(b);
  G[b].push_back(a);
}
G[N].push_back(0);

queue&lt;i64> que;
que.push(N);
idx[N] = vec.size();
vec.push_back(N);
while(!que.empty()) {
  i64 v = que.front();
  que.pop();
  for(auto x: G[v]) {
    if(idx[x] != -1) continue;
    que.push(x);
    idx[x] = vec.size();
    vec.push_back(x);
    p[x] = v;

    if(L1[v] == -1) L1[v] = idx[x];
    R1[v] = idx[x] + 1;

    i64 pp = p[v];
    if(pp != -1) {
      if(L2[pp] == -1) L2[pp] = idx[x];
      R2[pp] = idx[x] + 1;
    }
  }
}

わりと素直に書ける

# 感想

新出で驚いた典型にしていこうな