動的木上の最小シュタイナー木をtoptreeで解く

Last updated Dec 14, 2019

• Algorithm

この記事は「データ構造とアルゴリズム Advent Calendar 2019」 14日目の記事です.
13日目は@ajalabさんのRun-Length FM-Index - koki,
15日目は@minaminaoさんのMerkle Patricia Tree まわりです.

toptreeは今年競プロ界隈で話題になった動的木を扱うデータ構造の一つです.
link-cut treeも同じ動的木を扱うデータ構造ですが, 機能だけを見ればその完全上位互換です.

toptreeは, 木を動的に扱うデータ構造です. [cs/0310065] Maintaining Information in Fully-Dynamic Trees with Top Treesを読みました.

toptree自体については半年くらい前に自分が書いた記事があります.

Toptree 導入編 - niuez’s diary

上の記事をまとめると

• 基本的には, 平衡二分探索木(Splay Tree)
• 葉には辺を表すノード(Edge Node)
• 1頂点を共有する２つの辺をマージして新しくできた辺を平衡二分探索木の節とする(Compress & Rake)

• 二分木だけでは列しか管理できないので, 二分木ともう一つの子を管理する(Rake Node)

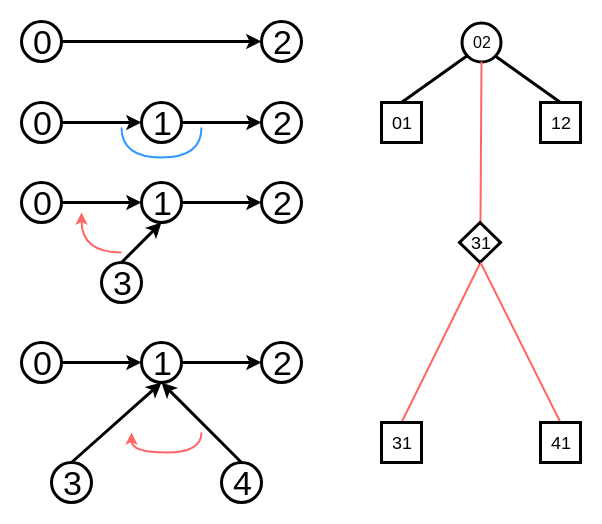
というあたりです. この形を保持しながらsplay treeの回転を行い各クエリの計算量を償却$ O(\log N)$を達成しています.

例えば,

• $ \mathtt{link}$: ある2頂点間を辺で結ぶ
• $ \mathtt{cut}$: ある2頂点間を結んでいる辺をなくす
• パス: ある木の2頂点を結ぶパスについてのクエリを処理する
  • 辺の重みの総和
  • 辺の重みを$ +x$する
  • など...
• 木全体に対するクエリ
  • 木に含まれる辺の重みを$ +x$する
  • 木の頂点の重みの総和
  • 木の直径
  • ある頂点からの最遠点距離
• toptree上の二分探索
  • 木の中心
  • 木の重心
  • パス$ x, \cdots, y$上で$ x$から$ y$に向かって$ d$だけ進んだ場所にある頂点 *1

というクエリが処理できます. 最強っぽい.

これを実装したのがこれです. めっちゃ大変でした. niuez/toptree-rust

10月に僕の作問した問題がyukicoderで木上クエリコンとして出題されました. このときに全問正解を(意図的に)阻止した問題がこれです.

No.902 Query ζone - yukicoder

辺に正の重みが与えられている木の形が動的に変わっていくなかで, 頂点$ v_0, \cdots, v_{k-1}$の最小シュタイナー木の重みを答えるクエリを処理しなければなりません.

サンプルを図にしてみます.

サンプルの2個目のクエリのとき, 木は以下のような形をしています. この木に関して, 頂点0, 4, 6を頂点の部分集合とする最小シュタイナー木の重みは20です.

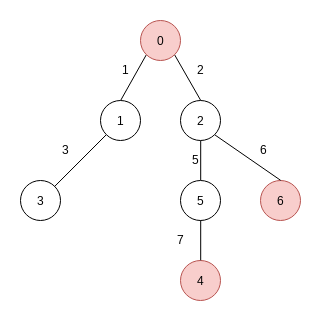
サンプルの4個目のクエリのとき, 木は以下のような形をしています. この木に関して, 頂点0, 4, 6を頂点の部分集合とする最小シュタイナー木の重みは27です.

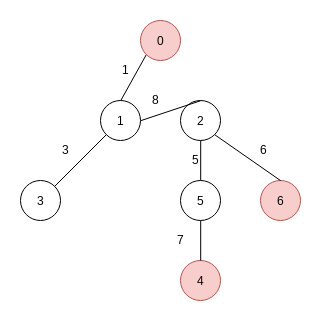
この問題は, toptreeに載せることで解くことができます. 今回はその解説をしたいと思います.

ここから先, 各クエリで最小シュタイナー木に含めなければならない頂点を赤い頂点と表現することにします.

toptreeでは上でも述べたように, 1頂点を共有する２つの辺をマージして新しくできた辺を平衡二分探索木の節とします.
今回の問題で考えられる, マージされる前の辺の状態は2通りのみです.

• 赤い頂点を1個以上含んでマージされた辺

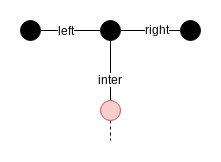
• 赤い頂点を一度も含んでいない辺

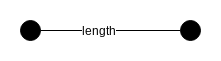
以下のような場合を考えそうになりますが, これは$ \mathbb{inter}=0$とすると, １つ目のパターンと同じになります.

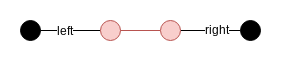
辺の端点の色は, マージするときに考えます. つまり, マージの方法は 左側の辺の状態(2通り) * 右側の辺の状態(2通り) * 共有している1頂点の色(2通り) = 8通りです

以下の通りです.

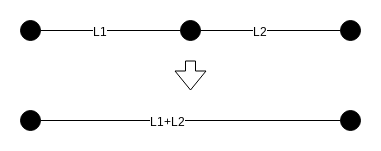
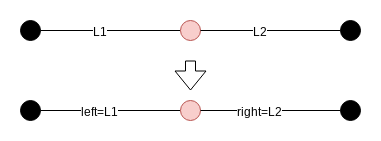
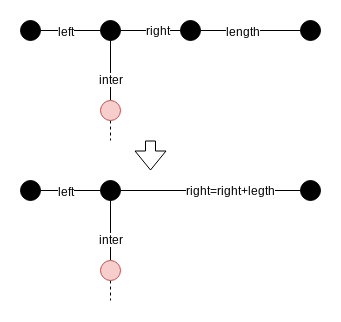
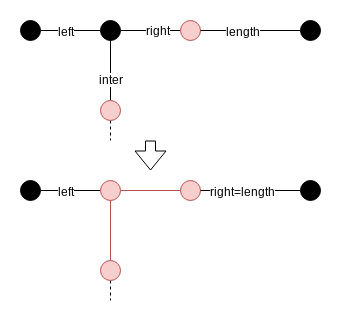
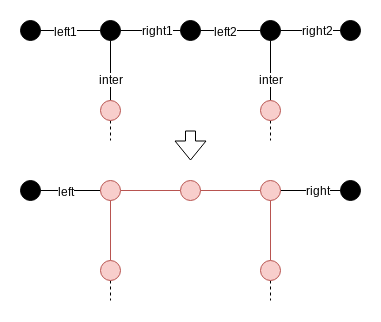
このパターンは頂点が赤でも黒でも同じです

このパターンだけでは, $ \mathbb{inter}$は作られません. どういうことでしょう…?
上でも述べたとおり, toptreeでは2通りのマージ方法があります. そのもう一つのマージ方法(Rake)では以下のパターンで$ \mathbb{inter}$を発生させます.

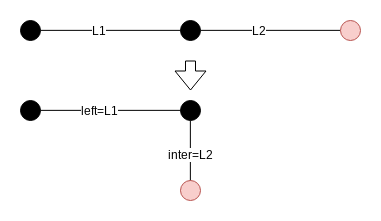
他のパターンは上と同じように計算することができます.

これをちゃんと実装すると以下のように解くことができます.

#383717 No.902 Query ζone - yukicoder

20行目からの関数が, 上で述べたCompressのマージの計算をしています. その下にRakeの計算もありますね.

今年はtoptreeに夢中な一年でした. 来年はどうなるでしょうか.